橋（bridge）検出アルゴリズム

連結グラフにおいて橋（bridge）とは、それを取り除くと連結でなくなってしまうような辺のこと。閉路に含まれない辺が橋になる。
橋はDFSを行うことで検出することができる。DFSは、アルゴリズムの一部としてグラフの構造を調べる時によく使われる。

アルゴリズム

まず、頂点を１つ選び、DFSを開始する。
各頂点には、pre、lowという２つのデータを記録する。
preは、DFS木の行きがけ順（pre-order）の値を保持する。
lowは、DFS木でその頂点から到達しうる頂点のpreの最小値を保持する。初期値はその頂点のpreである。

次の頂点が、すでに訪れてある（preの値が存在する）場合は、自分のlowを、次の頂点のlowと比べて小さい方に更新する。
次の頂点をまだ訪れていない場合は、その頂点に対してDFSを続ける。そして、その頂点へのDFSが終了した際に、lowがpreより小さくなっていれば、その頂点へ向かう辺は橋である。

例えば、次のような無向グラフがあるとする。

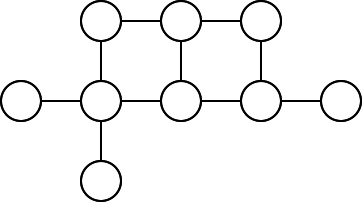
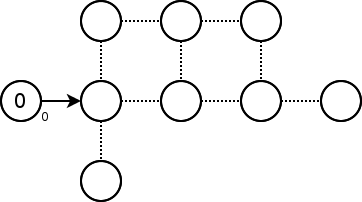
左端の頂点からDFSを始める。行きがけ順でpreの値を設定していく。
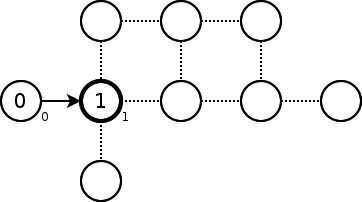
preの値を円内に、lowの値を右下に表示している。
以降、pre=Xの頂点を、頂点Xと呼ぶ。

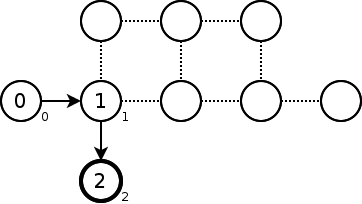
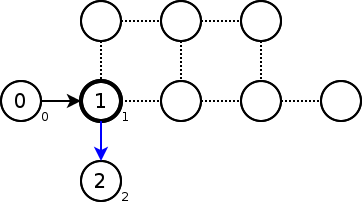
頂点2へのDFSが終了した。このときlow=pre=2となっている。つまり、頂点2より先はそこで完結しているということがわかる。したがって、頂点1->頂点2の辺を橋とする。
別の頂点へDFSを続ける。

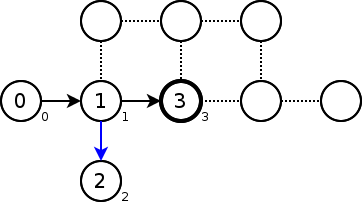
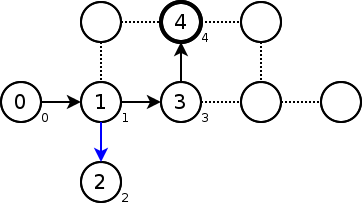
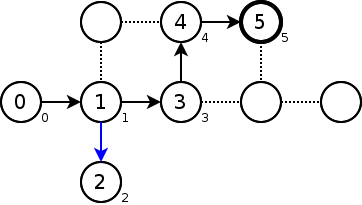
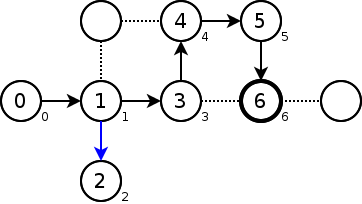
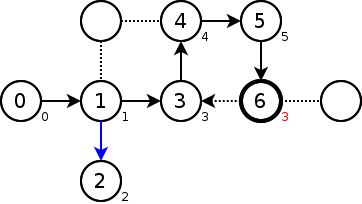
頂点3は既に訪れており、lowの値は当然小さい。頂点6のlowを3に更新する。

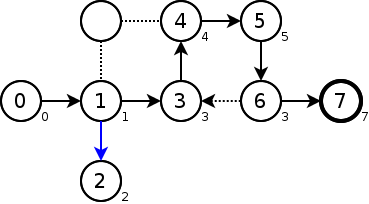
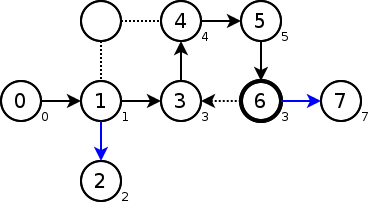
頂点7はlow=pre=7なので、頂点6->頂点7の辺は橋である。

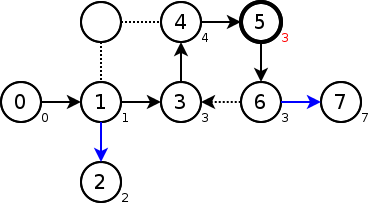
頂点6はlow=3<pre=6なので、頂点6->頂点7の辺は橋ではない。
DFSが終了する度に、親ノードのlowを更新していく。

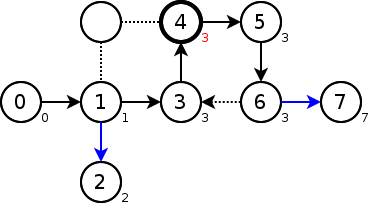
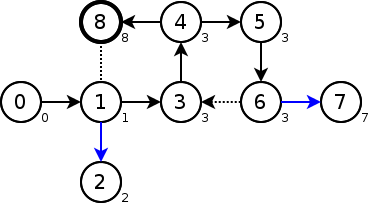
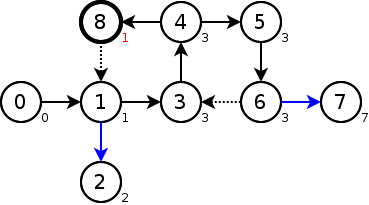
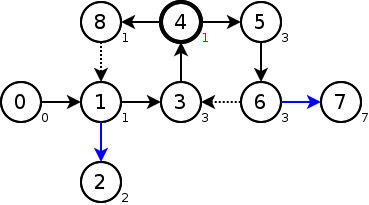
頂点4のlowの値が再び更新された。

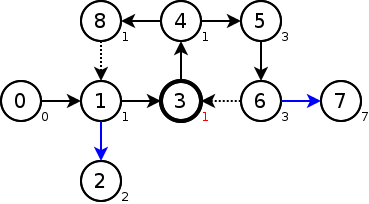
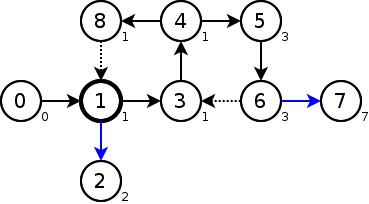
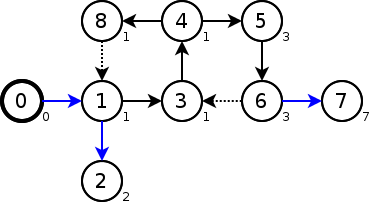
low=pre=1より頂点1の先で完結していることがわかるので、頂点0->頂点1を橋とする。

注意点として、親ノードが次の頂点である場合には特別な対処が必要だ。
無向グラフでは必ず双方向に辺が張っている。例えば、A->Bという辺があった場合、B->Aという辺も必ず存在する。しかし、これは閉路ではないので、無視しなければならない。
上の図では親ノードへの走査を省略している。

サンプルコード

typedef vector<int> VI;
typedef vector<VI> VVI;
typedef pair<int, int> PI;

// res: bridges
// v: current node
// from: parent node
int dfs(VVI& g, vector<PI>& res, int v, int& count, int from, VI& low, VI& pre) {
  pre[v] = count++;
  low[v] = pre[v];
  for (VI::iterator it = g[v].begin(); it != g[v].end(); it++) {
    int to = *it;
    if (pre[to] == -1) {
      // destination has not been visited
      // visit destination and update low[v]
      low[v] = min(low[v], dfs(g, res, to, count, v, low, pre));
      if (low[to] == pre[to]) {
        // edge is not contained in a closed path -> bridge
        res.push_back(make_pair(v, to));
      }
    } else {
      if (from == to) {
        // ignore a path to parent
        continue;
      }
      low[v] = min(low[v], low[to]);
    }
  }
  return low[v];
}

// Calculate bridges in a undirected graph.
// Assume graph is connected and has no parallel edges or self-loops.
// g: adjacency list
// V: number of nodes
vector<PI> bridges(VVI& g, int V) {
  vector<PI> res;
  if (V > 0) {
    // assume at least the first vertex exists
    VI low(V, -1);  // lowest reacheable index
    VI pre(V, -1);  // pre-order index
    int count = 0;  // pre-order index counter
    dfs(g, res, 0, count, -1, low, pre);  // start dfs from vertex 0
  }
  return res;
}

参考

• http://stackoverflow.com/questions/11218746/bridges-in-a-connected-graph
• Introduction to Algorithms, 3rd, Problem 22-2